According to the CCSSM, Kindergarten students should "fluently add and subtract within 5 (K.OA.5)" and "for any number from 1 to 9, find the number that makes 10 when added to the given number (K.OA.4)".

Number bonds help students see that numbers can be "broken" into pieces to make computation easier (decomposing/composing). With number bonds, students recognize the relationships between numbers through a written model that shows how the numbers are related. A number bond helps student clearly visualize the Part/Whole relationship.

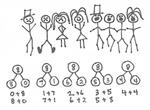
A number bond for the numbers 2, 3, and 5 might look like the model below.  Students will also see the whole on top with the parts branching down. The circles or squares are just a visual representation that students should begin with.  In first grade, some students may move away from the shape visual and opt for the carrot (upside down V).

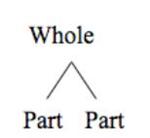
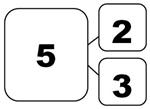
You might notice a similarity to fact families, and you'd be right.  There are a couple of differences, however. First, we often teach fact families through rote memorization only.  Kids can rattle off 2 + 3 = 5, 3 + 2 = 5, 5 - 2 = 3, and 5 - 3 = 2, but they often don't really understand how the addition and subtraction sentences are related.

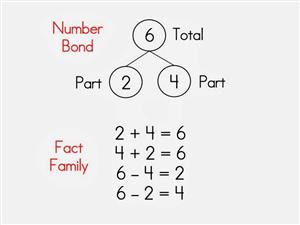
Second, we don't usually focus on all the fact families for a given number, for example 5. Through working with number bonds, children learn that 2 and 3 make 5, but so do 4 and 1.  In other words, they experience multiple ways to decompose the same number. Start out working with smaller numbers and gradually work toward larger ones, and of course the students will need LOTS of concrete practice.  The part/part/whole mat pictured below is a great tool.

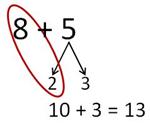
So let's look at this example, which shows one way a 1st Grade child might determine the sum of 8 and 5 ("add and subtract within 20...use strategies such as...making 10" 1.OA.6) using the skills he learned in Kindergarten. The student knows he wants 2 more to put with the 8 to make 10 (K.OA.4), and he knows he can decompose 5 into 2 and 3 (K.OA.5).  So now he is thinking of 10 + 3, or 13. 

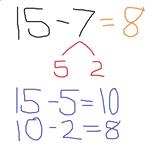
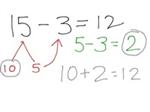
Let's move on to 2nd Grade, where students are expected to "add and subtract within 100 using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction (2.NBT.5)".  Now our student is faced with finding the sum of 37 and 25, which would normally be thought of as a "regrouping" problem.  This student is still looking to make 10s, so she knows she needs 3 more to make 37 into 40.  And notice that she is really still splitting 5, even though now it's actually 25.  After splitting, she's got an easy mental problem in 40 + 22.

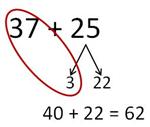
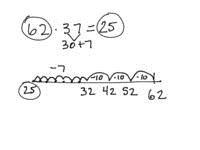
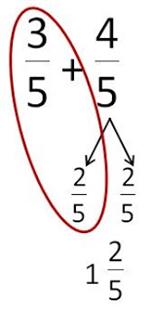
Let's move on to fractions.  In 4th grade, students must "decompose a fraction into a sum of fractions with the same denominator in more than one way (4.NF.3b)" and "add and subtract mixed numbers with like denominators (4.NF.3c)".  Let's see how our number bond knowledge can help here. We split the 4/5 into 2/5 and 2/5 (4.NF.3b) to create a whole out of the 3/5, resulting in 1 2/5 (4.NF.3c).  This is a bit more conceptual than finding an improper fraction and then introducing a totally different procedure for converting it to a mixed number. 

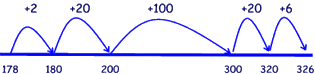
How about measurement?  Elapsed time maybe (3.MD.1)?  Doesn't this actually mirror what we do when we calculate elapsed time mentally?

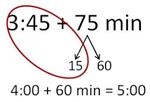
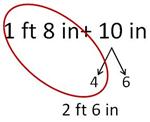
 Or adding and converting measurement units (4.MD.2)?

Multiplication and Division 4.NBT.5, 4.NBT.6 and 5.NBT.5, 5.NBT.6  

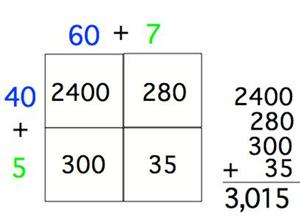
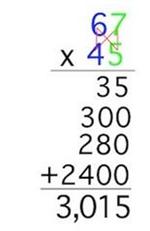
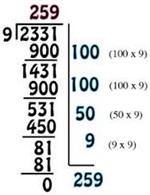
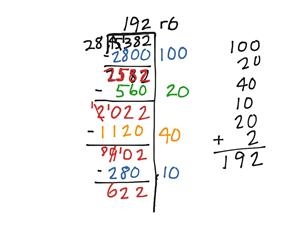
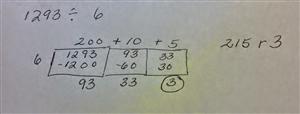
4.NBT.6 and 5.NBT.6  specifically mention the area model for division.

Notice that all of these examples require some form of decomposing and composing numbers (Distributive Property thinking) and that it all starts in Kindergarten! 

 CLICK HER FOR VIDEOS of NUMBER BONDS